Published online by Cambridge University Press: 08 March 2019
Let 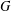 $G$ be a finite group and let
$G$ be a finite group and let 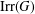 $\text{Irr}(G)$ be the set of all irreducible complex characters of
$\text{Irr}(G)$ be the set of all irreducible complex characters of 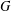 $G$. Let
$G$. Let 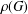 $\unicode[STIX]{x1D70C}(G)$ be the set of all prime divisors of character degrees of
$\unicode[STIX]{x1D70C}(G)$ be the set of all prime divisors of character degrees of 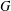 $G$. The character degree graph
$G$. The character degree graph 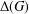 $\unicode[STIX]{x1D6E5}(G)$ associated to
$\unicode[STIX]{x1D6E5}(G)$ associated to 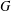 $G$ is a graph whose vertex set is
$G$ is a graph whose vertex set is 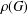 $\unicode[STIX]{x1D70C}(G)$, and there is an edge between two distinct primes
$\unicode[STIX]{x1D70C}(G)$, and there is an edge between two distinct primes 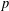 $p$ and
$p$ and 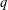 $q$ if and only if
$q$ if and only if 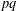 $pq$ divides
$pq$ divides 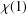 $\unicode[STIX]{x1D712}(1)$ for some
$\unicode[STIX]{x1D712}(1)$ for some 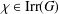 $\unicode[STIX]{x1D712}\in \text{Irr}(G)$. We prove that
$\unicode[STIX]{x1D712}\in \text{Irr}(G)$. We prove that 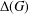 $\unicode[STIX]{x1D6E5}(G)$ is
$\unicode[STIX]{x1D6E5}(G)$ is 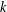 $k$-regular for some natural number
$k$-regular for some natural number 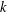 $k$ if and only if
$k$ if and only if 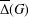 $\overline{\unicode[STIX]{x1D6E5}}(G)$ is a regular bipartite graph.
$\overline{\unicode[STIX]{x1D6E5}}(G)$ is a regular bipartite graph.