Article contents
ON SOME PROPERTIES OF QUASI-DISTANCE-BALANCED GRAPHS
Published online by Cambridge University Press: 30 January 2018
Abstract
For an edge 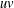 $uv$ in a graph
$uv$ in a graph 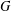 $G$ ,
$G$ , 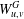 $W_{u,v}^{G}$ denotes the set of all vertices of
$W_{u,v}^{G}$ denotes the set of all vertices of 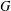 $G$ that are closer to
$G$ that are closer to  $u$ than to
$u$ than to  $v$ . A graph
$v$ . A graph 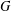 $G$ is said to be quasi-distance-balanced if there exists a constant
$G$ is said to be quasi-distance-balanced if there exists a constant 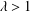 $\unicode[STIX]{x1D706}>1$ such that
$\unicode[STIX]{x1D706}>1$ such that 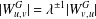 $|W_{u,v}^{G}|=\unicode[STIX]{x1D706}^{\pm 1}|W_{v,u}^{G}|$ for every pair of adjacent vertices
$|W_{u,v}^{G}|=\unicode[STIX]{x1D706}^{\pm 1}|W_{v,u}^{G}|$ for every pair of adjacent vertices  $u$ and
$u$ and  $v$ . The existence of nonbipartite quasi-distance-balanced graphs is an open problem. In this paper we investigate the possible structure of cycles in quasi-distance-balanced graphs and generalise the previously known result that every quasi-distance-balanced graph is triangle-free. We also prove that a connected quasi-distance-balanced graph admitting a bridge is isomorphic to a star. Several open problems are posed.
$v$ . The existence of nonbipartite quasi-distance-balanced graphs is an open problem. In this paper we investigate the possible structure of cycles in quasi-distance-balanced graphs and generalise the previously known result that every quasi-distance-balanced graph is triangle-free. We also prove that a connected quasi-distance-balanced graph admitting a bridge is isomorphic to a star. Several open problems are posed.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by

