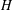 $H$-ANTIMAGICNESS OF DISCONNECTED GRAPHS
$H$-ANTIMAGICNESS OF DISCONNECTED GRAPHSPublished online by Cambridge University Press: 01 April 2016
A simple graph 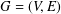 $G=(V,E)$ admits an
$G=(V,E)$ admits an 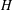 $H$-covering if every edge in
$H$-covering if every edge in 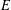 $E$ belongs to at least one subgraph of
$E$ belongs to at least one subgraph of 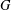 $G$ isomorphic to a given graph
$G$ isomorphic to a given graph 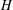 $H$. Then the graph
$H$. Then the graph 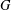 $G$ is
$G$ is 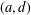 $(a,d)$-
$(a,d)$-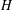 $H$-antimagic if there exists a bijection
$H$-antimagic if there exists a bijection 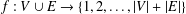 $f:V\cup E\rightarrow \{1,2,\ldots ,|V|+|E|\}$ such that, for all subgraphs
$f:V\cup E\rightarrow \{1,2,\ldots ,|V|+|E|\}$ such that, for all subgraphs  $H^{\prime }$ of
$H^{\prime }$ of 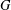 $G$ isomorphic to
$G$ isomorphic to 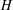 $H$, the
$H$, the  $H^{\prime }$-weights,
$H^{\prime }$-weights, 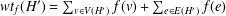 $wt_{f}(H^{\prime })=\sum _{v\in V(H^{\prime })}f(v)+\sum _{e\in E(H^{\prime })}f(e)$, form an arithmetic progression with the initial term
$wt_{f}(H^{\prime })=\sum _{v\in V(H^{\prime })}f(v)+\sum _{e\in E(H^{\prime })}f(e)$, form an arithmetic progression with the initial term  $a$ and the common difference
$a$ and the common difference 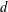 $d$. When
$d$. When 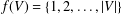 $f(V)=\{1,2,\ldots ,|V|\}$, then
$f(V)=\{1,2,\ldots ,|V|\}$, then  $G$ is said to be super
$G$ is said to be super  $(a,d)$-
$(a,d)$- $H$-antimagic. In this paper, we study super
$H$-antimagic. In this paper, we study super  $(a,d)$-
$(a,d)$- $H$-antimagic labellings of a disjoint union of graphs for
$H$-antimagic labellings of a disjoint union of graphs for 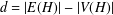 $d=|E(H)|-|V(H)|$.
$d=|E(H)|-|V(H)|$.