Article contents
HYPERPLANES OF FINITE-DIMENSIONAL NORMED SPACES WITH THE MAXIMAL RELATIVE PROJECTION CONSTANT
Published online by Cambridge University Press: 02 March 2015
Abstract
The relative projection constant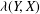 ${\it\lambda}(Y,X)$ of normed spaces
${\it\lambda}(Y,X)$ of normed spaces 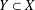 $Y\subset X$ is
$Y\subset X$ is 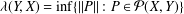 ${\it\lambda}(Y,X)=\inf \{\Vert P\Vert :P\in {\mathcal{P}}(X,Y)\}$, where
${\it\lambda}(Y,X)=\inf \{\Vert P\Vert :P\in {\mathcal{P}}(X,Y)\}$, where 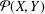 ${\mathcal{P}}(X,Y)$ denotes the set of all continuous projections from
${\mathcal{P}}(X,Y)$ denotes the set of all continuous projections from 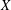 $X$ onto
$X$ onto 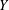 $Y$. By the well-known result of Bohnenblust, for every
$Y$. By the well-known result of Bohnenblust, for every  $n$-dimensional normed space
$n$-dimensional normed space 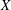 $X$ and a subspace
$X$ and a subspace 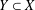 $Y\subset X$ of codimension one,
$Y\subset X$ of codimension one, 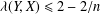 ${\it\lambda}(Y,X)\leq 2-2/n$. The main goal of the paper is to study the equality case in the theorem of Bohnenblust. We establish an equivalent condition for the equality
${\it\lambda}(Y,X)\leq 2-2/n$. The main goal of the paper is to study the equality case in the theorem of Bohnenblust. We establish an equivalent condition for the equality 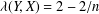 ${\it\lambda}(Y,X)=2-2/n$ and present several applications. We prove that every three-dimensional space has a subspace with the projection constant less than
${\it\lambda}(Y,X)=2-2/n$ and present several applications. We prove that every three-dimensional space has a subspace with the projection constant less than 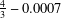 $\frac{4}{3}-0.0007$. This gives a nontrivial upper bound in the problem posed by Bosznay and Garay. In the general case, we give an upper bound for the number of (
$\frac{4}{3}-0.0007$. This gives a nontrivial upper bound in the problem posed by Bosznay and Garay. In the general case, we give an upper bound for the number of (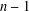 $n-1$)-dimensional subspaces with the maximal relative projection constant in terms of the facets of the unit ball of
$n-1$)-dimensional subspaces with the maximal relative projection constant in terms of the facets of the unit ball of 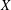 $X$. As a consequence, every
$X$. As a consequence, every  $n$-dimensional normed space
$n$-dimensional normed space 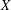 $X$ has an (
$X$ has an (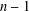 $n-1$)-dimensional subspace
$n-1$)-dimensional subspace 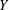 $Y$ with
$Y$ with 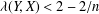 ${\it\lambda}(Y,X)<2-2/n$. This contrasts with the separable case in which it is possible that every hyperplane has a maximal possible projection constant.
${\it\lambda}(Y,X)<2-2/n$. This contrasts with the separable case in which it is possible that every hyperplane has a maximal possible projection constant.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

