No CrossRef data available.
Article contents
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF 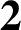 $\textbf{2}$ AND
$\textbf{2}$ AND 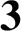 $\textbf{3}$
$\textbf{3}$
Published online by Cambridge University Press: 14 January 2021
Abstract
Andrews introduced the partition function 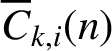 $\overline {C}_{k, i}(n)$, called the singular overpartition function, which counts the number of overpartitions of n in which no part is divisible by k and only parts
$\overline {C}_{k, i}(n)$, called the singular overpartition function, which counts the number of overpartitions of n in which no part is divisible by k and only parts 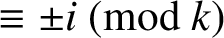 $\equiv \pm i\pmod {k}$ may be overlined. We prove that
$\equiv \pm i\pmod {k}$ may be overlined. We prove that 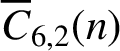 $\overline {C}_{6, 2}(n)$ is almost always divisible by
$\overline {C}_{6, 2}(n)$ is almost always divisible by 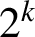 $2^k$ for any positive integer k. We also prove that
$2^k$ for any positive integer k. We also prove that 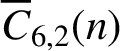 $\overline {C}_{6, 2}(n)$ and
$\overline {C}_{6, 2}(n)$ and 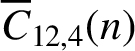 $\overline {C}_{12, 4}(n)$ are almost always divisible by
$\overline {C}_{12, 4}(n)$ are almost always divisible by 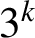 $3^k$. Using a result of Ono and Taguchi on nilpotency of Hecke operators, we find infinite families of congruences modulo arbitrary powers of
$3^k$. Using a result of Ono and Taguchi on nilpotency of Hecke operators, we find infinite families of congruences modulo arbitrary powers of 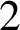 $2$ satisfied by
$2$ satisfied by 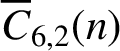 $\overline {C}_{6, 2}(n)$.
$\overline {C}_{6, 2}(n)$.
MSC classification
Secondary:
05A17: Partitions of integers
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 238 - 248
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
Andrews, G. E., ‘Singular overpartitions’, Int. J. Number Theory 11 (2015), 1523–1533.CrossRefGoogle Scholar
Aricheta, V. M., ‘Congruences for Andrews’
 $\left(k,i\right)$
-singular overpartitions’, Ramanujan J. 43 (2017), 535–549.CrossRefGoogle Scholar
$\left(k,i\right)$
-singular overpartitions’, Ramanujan J. 43 (2017), 535–549.CrossRefGoogle Scholar
Barman, R. and Ray, C., ‘Divisibility of Andrews’ singular overpartitions by powers of 2 and
 $3$
’, Res. Number Theory 5 (2019), 22.CrossRefGoogle Scholar
$3$
’, Res. Number Theory 5 (2019), 22.CrossRefGoogle Scholar
Chen, S. C., Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic properties of Andrews’ singular overpartitions’, Int. J. Number Theory 11 (2015), 1463–1476.CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J., ‘Overpartitions’, Trans. Amer. Math. Soc. 356 (2004), 1623–1635.CrossRefGoogle Scholar
Koblitz, N., Introduction to Elliptic Curves and Modular Forms (Springer-Verlag, New York, 1991).Google Scholar
Ono, K., ‘Parity of the partition function in arithmetic progressions’, J. reine angew. Math. 472 (1996), 1–15.Google Scholar
Ono, K., The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and
 $q$
-Series, CBMS Regional Conference Series in Mathematics, 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
$q$
-Series, CBMS Regional Conference Series in Mathematics, 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Ono, K. and Taguchi, Y., ‘2-adic properties of certain modular forms and their applications to arithmetic functions’, Int. J. Number Theory 1 (2005), 75–101.CrossRefGoogle Scholar
Serre, J.-P., ‘Divisibilité de certaines fonctions arithmétiques’, Séminaire Delange-Pisot-Poitou. Théorie des Nombres 16 (1974), 1–28.Google Scholar
Serre, J.-P., ‘Valeurs propres des opérateurs de Hecke modulo
 $\ell$
’, Astérisque 24 (1975), 109–117.Google Scholar
$\ell$
’, Astérisque 24 (1975), 109–117.Google Scholar
Tate, J., ‘Extensions of
 $\mathbb{Q}$
unramified outside 2’, In: Arithmetic Geometry: Conference on Arithmetic Geometry with an Emphasis on Iwasawa Theory, March 15–18, 1993, Arizona State University, Contemporary Mathematics, 174 (American Mathematical Society, Providence, RI, 1994).CrossRefGoogle Scholar
$\mathbb{Q}$
unramified outside 2’, In: Arithmetic Geometry: Conference on Arithmetic Geometry with an Emphasis on Iwasawa Theory, March 15–18, 1993, Arizona State University, Contemporary Mathematics, 174 (American Mathematical Society, Providence, RI, 1994).CrossRefGoogle Scholar


