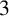Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ZHANG, JUNYANG
and
TAO, YING
2023.
NOWHERE-ZERO -FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 107,
Issue. 3,
p.
353.
Zhang, Junyang
and
Zhou, Sanming
2024.
Nowhere-zero 3-flows in Cayley graphs on supersolvable groups.
Journal of Combinatorial Theory, Series A,
Vol. 204,
Issue. ,
p.
105852.
Zhang, Junyang
and
Zhou, Sanming
2024.
Nowhere-zero 3-flows in nilpotently vertex-transitive graphs.
Journal of Algebraic Combinatorics,
Vol. 60,
Issue. 1,
p.
225.