Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T18:51:14.961Z Has data issue: false hasContentIssue false
  • English
  • Français

LONGEST CYCLES AND LONGEST CHORDLESS CYCLES IN 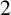$2$-CONNECTED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  27 February 2025

YANAN HU Open the ORCID record for YANAN HU [Opens in a new window] ,
CHENGLI LI Open the ORCID record for CHENGLI LI [Opens in a new window]  and
FENG LIU Open the ORCID record for FENG LIU [Opens in a new window]
YANAN HU
Affiliation:
School of Science, Shanghai Institute of Technology, Shanghai 201418, PR China e-mail: hg@sit.edu.cn
CHENGLI LI*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200241, PR China
FENG LIU
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200241, PR China e-mail: fengl69@stu.ecnu.edu.cn
*
e-mail: lichengli0130@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Thomassen’s chord conjecture from 1976 states that every longest cycle in a 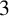$3$-connected graph has a chord. The circumference 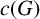$c(G)$ and induced circumference 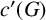$c'(G)$ of a graph G are the length of its longest cycles and the length of its longest chordless cycles, respectively. Harvey [‘A cycle of maximum order in a graph of high minimum degree has a chord’, Electron. J. Combin. 24(4) (2017), Article no. 4.33, 8 pages] proposed the stronger conjecture: every $2$-connected graph G with minimum degree at least $3$ has 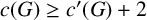$c(G)\geq c'(G)+2$. This conjecture implies Thomassen’s chord conjecture. We observe that wheels are the unique Hamiltonian graphs for which the circumference and the induced circumference differ by exactly one. Thus, we need only consider non-Hamiltonian graphs for Harvey’s conjecture. We propose a conjecture involving wheels that is equivalent to Harvey’s conjecture on non-Hamiltonian graphs. A graph is 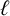$\ell $-holed if all its holes have length exactly 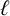$\ell $. We prove that Harvey’s conjecture and hence also Thomassen’s conjecture hold for $\ell $-holed graphs and graphs with a small induced circumference.

Keywords

longest cyclelongest chordless cycleℓ-holedwheels

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C38: Paths and cycles 05C40: Connectivity
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported by the NSFC grant 12271170 and Science and Technology Commission of Shanghai Municipality (STCSM) grant 22DZ2229014.

References

Alspach, B. R. and Godsil, C. D. (eds.), ‘Unsolved problems’, in: Cycles in Graphs, Annals of Discrete Mathematics, 27 (North-Holland, Amsterdam, 1985), 461–467.Google Scholar
Birmelé, E., ‘Every longest circuit of a 3-connected, ${K}_{3,3}$ -minor free graph has a chord’, J. Graph Theory 58 (2008), 293–298.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, New York, 2008).CrossRefGoogle Scholar
Cook, L., Horsfield, J., Preissmann, M., Robin, C., Seymour, P., Sintiari, N. L. D., Trotignon, N. and Vuǎković, K., ‘Graphs with all holes the same length’, J. Combin. Theory Ser. B 168 (2024), 96–158.CrossRefGoogle Scholar
Harvey, D. J., ‘A cycle of maximum order in a graph of high minimum degree has a chord’, Electron. J. Combin. 24(4) (2017), Article no. 4.33, 8 pages.CrossRefGoogle Scholar
Kawarabayashi, K., Niu, J. and Zhang, C. Q., ‘Chords of longest circuits in locally planar graphs’, European J. Combin. 28 (2007), 315–321.CrossRefGoogle Scholar
Li, X. and Zhang, C. Q., ‘Chords of longest circuits in 3-connected graphs’, Discrete Math. 268 (2003), 199–206.CrossRefGoogle Scholar
Li, X. and Zhang, C. Q., ‘Chords of longest circuits of graphs embedded in torus and Klein bottle’, J. Graph Theory 43 (2003), 1–23.CrossRefGoogle Scholar
Thomassen, C., ‘Configurations in graphs of large minimum degree, connectivity, or chromatic number’, Ann. New York Acad. Sci. 555 (1989), 402–412.CrossRefGoogle Scholar
Thomassen, C., ‘Chords of longest cycles in cubic graphs’, J. Combin. Theory Ser. B 71 (1997), 211–214.CrossRefGoogle Scholar
Thomassen, C., ‘Chords in longest cycles’, J. Combin. Theory Ser. B 129 (2018), 148–157.CrossRefGoogle Scholar
West, D. B., Introduction to Graph Theory (Prentice Hall, Denver, CO, 1996).Google Scholar
Wu, J., Broersma, H. and Kang, H., ‘Removable edges and chords of longest cycles in 3-connected graphs’, Graphs Combin. 30 (2014), 743–753.CrossRefGoogle Scholar
Zhang, C. Q., ‘Longest cycles and their chords’, J. Graph Theory 11 (1987), 521–529.CrossRefGoogle Scholar