Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Komjáthy, Júlia
and
Lodewijks, Bas
2020.
Explosion in weighted hyperbolic random graphs and geometric inhomogeneous random graphs.
Stochastic Processes and their Applications,
Vol. 130,
Issue. 3,
p.
1309.
Fountoulakis, Nikolaos
and
Yukich, Joseph
2020.
Limit theory for isolated and extreme points in hyperbolic random geometric graphs.
Electronic Journal of Probability,
Vol. 25,
Issue. none,
Zheng, Muhua
García-Pérez, Guillermo
Boguñá, Marián
and
Serrano, M. Ángeles
2021.
Scaling up real networks by geometric branching growth.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 21,
Diel, Roland
and
Mitsche, Dieter
2021.
On the largest component of subcritical random hyperbolic graphs.
Electronic Communications in Probability,
Vol. 26,
Issue. none,
Linker, Amitai
Mitsche, Dieter
Schapira, Bruno
and
Valesin, Daniel
2021.
The contact process on random hyperbolic graphs: Metastability and critical exponents.
The Annals of Probability,
Vol. 49,
Issue. 3,
Boguñá, Marián
Bonamassa, Ivan
De Domenico, Manlio
Havlin, Shlomo
Krioukov, Dmitri
and
Serrano, M. Ángeles
2021.
Network geometry.
Nature Reviews Physics,
Vol. 3,
Issue. 2,
p.
114.
Herold, Felix
Hug, Daniel
and
Thäle, Christoph
2021.
Does a central limit theorem hold for the k-skeleton of Poisson hyperplanes in hyperbolic space?.
Probability Theory and Related Fields,
Vol. 179,
Issue. 3-4,
p.
889.
Fountoulakis, Nikolaos
van der Hoorn, Pim
Müller, Tobias
and
Schepers, Markus
2021.
Clustering in a hyperbolic model of complex networks.
Electronic Journal of Probability,
Vol. 26,
Issue. none,
Chellig, Jordan
Fountoulakis, Nikolaos
Skerman, Fiona
and
Van Mieghem, Piet
2021.
The modularity of random graphs on the hyperbolic plane.
Journal of Complex Networks,
Vol. 10,
Issue. 1,
van der Kolk, Jasper
Serrano, M. Ángeles
and
Boguñá, Marián
2022.
An anomalous topological phase transition in spatial random graphs.
Communications Physics,
Vol. 5,
Issue. 1,
Owada, Takashi
and
Yogeshwaran, D.
2022.
Sub-tree counts on hyperbolic random geometric graphs.
Advances in Applied Probability,
Vol. 54,
Issue. 4,
p.
1032.
Bläsius, Thomas
Freiberger, Cedric
Friedrich, Tobias
Katzmann, Maximilian
Montenegro-Retana, Felix
and
Thieffry, Marianne
2022.
Efficient Shortest Paths in Scale-Free Networks with Underlying Hyperbolic Geometry.
ACM Transactions on Algorithms,
Vol. 18,
Issue. 2,
p.
1.
Jankowski, Robert
Allard, Antoine
Boguñá, Marián
and
Serrano, M. Ángeles
2023.
The D-Mercator method for the multidimensional hyperbolic embedding of real networks.
Nature Communications,
Vol. 14,
Issue. 1,
Bläsius, Thomas
Friedrich, Tobias
Göbel, Andreas
Levy, Jordi
and
Rothenberger, Ralf
2023.
The impact of heterogeneity and geometry on the proof complexity of random satisfiability.
Random Structures & Algorithms,
Vol. 63,
Issue. 4,
p.
885.
van der Kolk, Jasper
García-Pérez, Guillermo
Kouvaris, Nikos E.
Serrano, M. Ángeles
and
Boguñá, Marián
2023.
Emergence of Geometric Turing Patterns in Complex Networks.
Physical Review X,
Vol. 13,
Issue. 2,
Bläsius, Thomas
Friedrich, Tobias
and
Katzmann, Maximilian
2023.
Efficiently Approximating Vertex Cover on Scale-Free Networks with Underlying Hyperbolic Geometry.
Algorithmica,
Vol. 85,
Issue. 12,
p.
3487.
van der Kolk, Jasper
Boguñá, Marián
and
Serrano, M. Ángeles
2024.
Renormalization of networks with weak geometric coupling.
Physical Review E,
Vol. 110,
Issue. 3,
van der Kolk, Jasper
Serrano, M. Ángeles
and
Boguñá, Marián
2024.
Random graphs and real networks with weak geometric coupling.
Physical Review Research,
Vol. 6,
Issue. 1,
Kiwi, Marcos
Schepers, Markus
and
Sylvester, John
2024.
Cover and hitting times of hyperbolic random graphs.
Random Structures & Algorithms,
Vol. 65,
Issue. 4,
p.
915.
Bringmann, Karl
Keusch, Ralph
and
Lengler, Johannes
2025.
Average distance in a general class of scale-free networks.
Advances in Applied Probability,
Vol. 57,
Issue. 2,
p.
371.
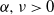 $\alpha, \nu > 0$, which we think of as constant. Roughly speaking,
$\alpha, \nu > 0$, which we think of as constant. Roughly speaking,  $\alpha$ controls the power-law exponent of the degree sequence and
$\alpha$ controls the power-law exponent of the degree sequence and  $\nu$ the average degree. Earlier work of Kiwi and Mitsche (2015) has shown that, when
$\nu$ the average degree. Earlier work of Kiwi and Mitsche (2015) has shown that, when 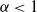 $\alpha \lt 1$ (which corresponds to the exponent of the power law degree sequence being
$\alpha \lt 1$ (which corresponds to the exponent of the power law degree sequence being 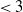 $\lt 3$), the diameter of the largest component is asymptotically almost surely (a.a.s.) at most polylogarithmic in N. Friedrich and Krohmer (2015) showed it was a.a.s.
$\lt 3$), the diameter of the largest component is asymptotically almost surely (a.a.s.) at most polylogarithmic in N. Friedrich and Krohmer (2015) showed it was a.a.s.  $\Omega(\log N)$ and improved the exponent of the polynomial in
$\Omega(\log N)$ and improved the exponent of the polynomial in 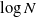 $\log N$ in the upper bound. Here we show the maximum diameter over all components is a.a.s.
$\log N$ in the upper bound. Here we show the maximum diameter over all components is a.a.s. 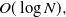 $O(\log N),$ thus giving a bound that is tight up to a multiplicative constant.
$O(\log N),$ thus giving a bound that is tight up to a multiplicative constant.
