Hostname: page-component-5b777bbd6c-7sgmh Total loading time: 0 Render date: 2025-06-20T11:41:42.260Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Properties of Estimators for the Parameters of Spatial Inhomogeneous Poisson Point Processes

Part of: Distribution theory Stochastic processes Inference from stochastic processes Parametric inference

Published online by Cambridge University Press:  01 July 2016

Stephen L. Rathbun  and
Noel Cressie
Stephen L. Rathbun*
Affiliation:
University of Georgia
Noel Cressie*
Affiliation:
Iowa State University
*
* Postal address: Department of Statistics, University of Georgia, Athens, GA 30602–1952, USA.
** Postal address: Statistical Laboratory and Department of Statistics, Snedecor Hall, Ames, IA 50011–1210, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

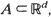Consider a spatial point pattern realized from an inhomogeneous Poisson process on a bounded Borel set , with intensity function λ (s; θ), where 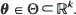. In this article, we show that the maximum likelihood estimator 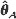and the Bayes estimator 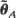are consistent, asymptotically normal, and asymptotically efficient as the sample region 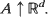. These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0, T] 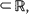, where T →∞. They also formalize (and extend to the multiparameter case) results announced by Krickeberg (1982), for the spatial domain 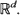. Furthermore, a Cramér–Rao lower bound is found for any estimator 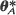of θ. The asymptotic properties of 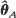and 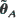are considered for modulated (Cox (1972)), and linear Poisson processes.

Keywords

SPATIAL POINT PROCESSMAXIMUM LIKELIHOOD ESTIMATORBAYES ESTIMATORCONSISTENCYASYMPTOTIC NORMALITYASYMPTOTIC EFFICIENCYMODULATED POISSON PROCESSCRAMÉR–RAO INEQUALITY

MSC classification

Primary: 62M09: Non-Markovian processes
Secondary: 60G55: Point processes 62E20: Asymptotic distribution theory 62F12: Asymptotic properties of estimators
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 26 , Issue 1 , March 1994 , pp. 122 - 154
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berger, M. S. (1977) Nonlinearity and Functional Analysis. Academic Press, New York.Google Scholar
Berman, M. (1986) Testing for spatial association between a point process and another stochastic process. Appl. Statist. 35, 54–62.CrossRefGoogle Scholar
Cox, D. R. (1972) The statistical analysis of dependencies in point processes. In Stochastic Point Processes, ed. Lewis, P. A. W., pp. 55–66. Wiley, New York.Google Scholar
Daley, D. J. and Vere-Jones, D. (1988) An Introduction to the Theory of Point Processes. Springer-Verlag, New York.Google Scholar
Fiksel, T. (1984) Simple spatial-temporal models for sequences of geological events. Electronische Informationsverarbeitung und Kybernetik (EIK) 20, 480–487.Google Scholar
Graybill, F. A. (1983) Matrices with Applications in Statistics, 2nd edn. Wadsworth, Belmont, CA.Google Scholar
Hájek, J. (1972) Local asymptotic minimax and admissibility in estimation. Proc. 6th Berkeley Symp. Math. Statist. Prob. 1, 175–194.Google Scholar
Ibragimov, I. A. and Has'Minskii, R. Z. (1975) Local asymptotic normality for non-identically distributed observations. Theory Prob. Appl. 20, 246–260.CrossRefGoogle Scholar
Ibragimov, I. A. and Has'Minskii, R. Z. (1981) Statistical Estimation. Asymptotic Theory. Springer-Verlag, New York.Google Scholar
Jensen, J. L. (1990) Asymptotic normality of estimates in spatial point processes. Research Report No. 210, Department of Theoretical Statistics, University of Aarhus.Google Scholar
Kooijman, S. A. L. M. (1979) The description of point patterns. In Spatial and Temporal Analysis in Ecology, ed. Cormack, R. M. and Ord, J. K., pp. 305–331. International Co-operative Publishing House, Fairland, MD.Google Scholar
Krickeberg, K. (1982) Processus ponctuels en statistique. In École d'Été de Probabilités de Saint-Flour X, ed. Hennequin, P. L., pp. 205–313. Lecture Notes in Mathematics 929, Springer-Verlag, Berlin.Google Scholar
Kutoyants, Yu. A. (1984) Parameter Estimation for Stochastic Processes. Heldermann Verlag, Berlin.Google Scholar
Lawson, A. (1988). On tests for spatial trend in a nonhomogeneous Poisson process. J. Appl. Statist. 15, 225–234.Google Scholar
Liptser, R. S. and Shiryayev, A. N. (1978) Statistics of Random Processes II. Applications. Springer-Verlag, New York.Google Scholar
Mase, S. (1992) Uniform LAN condition of planar Gibbsian point processes and optimality of maximum likelihood estimators of soft-core potential functions. Prob. Theory Rel. Fields 92, 51–67.Google Scholar
Ogata, Y. (1978) The asymptotic behavior of maximum likelihood estimators for stationary point processes. Ann. Inst. Statist. Math. 30A, 243–261.Google Scholar
Ogata, Y. and Katsura, K. (1986) Point-process models with linearly parameterized intensity for application to earthquake data. J. Appl. Prob. 23A, 291–310.Google Scholar
Ogata, Y. and Tanemura, M. (1981) Estimation of interaction potentials of spatial point patterns through the maximum likelihood procedure. Ann. Inst. Statist. Math. 33, 315–338.Google Scholar
Ogata, Y. and Tanemura, M. (1984) Likelihood analysis of spatial point patterns. J. R. Statist. Soc. B 46, 496–518.Google Scholar
Ogata, Y. and Tanemura, M. (1986) Likelihood estimation of interaction potentials and external fields of inhomogeneous spatial point processes. In Pacific Statistical Congress, ed. Francis, I. S., Manly, B. F. J. and Lam, F. C., pp. 150–154. Elsevier, Amsterdam.Google Scholar
Penttinen, A. (1984) Modelling interaction in spatial point patterns: parameter estimation by the maximum likelihood method. Jyväskylä Studies in Computer Science, Economics and Statistics 7, 1–107.Google Scholar
Rosenthal, H. P. (1970) On the subspaces of Lp (p > 2) spanned by sequences of independent random variables. Israel J. Math. 8, 273–303.Google Scholar
Royden, H. L. (1968) Real Analysis, 2nd edn. Macmillan, New York.Google Scholar
Vere-Jones, D. (1968) Some applications of probability generating functionals to the study of input-output streams. J. R. Statist. Soc. B 30, 321–333.Google Scholar
Wald, A. (1943) Tests of statistical hypotheses concerning several parameters when the number of observations is large. Trans. Amer. Math. Soc. 54, 426–482.Google Scholar
Westcott, M. (1972) The probability generating functional. J. Austral. Math. Soc. 14, 448–466.Google Scholar