Article contents
The Moment-SOS hierarchy: Applications and related topics
Published online by Cambridge University Press: 04 September 2024
Abstract
The Moment-SOS hierarchy, first introduced in optimization in 2000, is based on the theory of the S-moment problem and its dual counterpart: polynomials that are positive on S. It turns out that this methodology can also be used to solve problems with positivity constraints ‘f(x) ≥ 0 for all $\mathbf{x}\in S$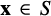 ’ or linear constraints on Borel measures. Such problems can be viewed as specific instances of the generalized moment problem (GMP), whose list of important applications in various domains of science and engineering is almost endless. We describe this methodology in optimization and also in two other applications for illustration. Finally we also introduce the Christoffel function and reveal its links with the Moment-SOS hierarchy and positive polynomials.
’ or linear constraints on Borel measures. Such problems can be viewed as specific instances of the generalized moment problem (GMP), whose list of important applications in various domains of science and engineering is almost endless. We describe this methodology in optimization and also in two other applications for illustration. Finally we also introduce the Christoffel function and reveal its links with the Moment-SOS hierarchy and positive polynomials.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 4
- Cited by

