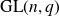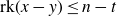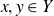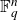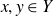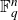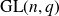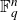Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
10 - Strong coupling
-
- Book:
- Quarks, Gluons and Lattices
- Published online:
- 05 November 2022
- Print publication:
- 16 February 2023, pp 60-76
-
- Chapter
-
- You have access
- Open access
- Export citation
Preface to 50th Anniversary Edition
-
-
- Book:
- The Large Scale Structure of Space-Time
- Published online:
- 17 February 2023
- Print publication:
- 16 February 2023, pp xiii-xviii
-
- Chapter
- Export citation
4 - Maxwell theory
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp 88-112
-
- Chapter
-
- You have access
- Open access
- Export citation
Dedication
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp vii-viii
-
- Chapter
-
- You have access
- Open access
- Export citation
Contents
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp ix-xii
-
- Chapter
-
- You have access
- Open access
- Export citation
Foreword
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp xiii-xiv
-
- Chapter
-
- You have access
- Open access
- Export citation
References
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp 545-566
-
- Chapter
-
- You have access
- Open access
- Export citation
Appendix C - Useful formulae
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp 535-544
-
- Chapter
-
- You have access
- Open access
- Export citation
References
-
- Book:
- The Large Scale Structure of Space-Time
- Published online:
- 17 February 2023
- Print publication:
- 16 February 2023, pp 373-380
-
- Chapter
- Export citation
13 - Asymptotic freedom and dimensional transmutation
-
- Book:
- Quarks, Gluons and Lattices
- Published online:
- 05 November 2022
- Print publication:
- 16 February 2023, pp 88-93
-
- Chapter
-
- You have access
- Open access
- Export citation
Intersection theorems for finite general linear groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 129-160
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
A subset Y of the general linear group
$\text{GL}(n,q)$ is called t-intersecting if 
$\text{rk}(x-y)\le n-t$ for all 
$x,y\in Y$, or equivalently x and y agree pointwise on a t-dimensional subspace of 
$\mathbb{F}_q^n$ for all 
$x,y\in Y$. We show that, if n is sufficiently large compared to t, the size of every such t-intersecting set is at most that of the stabiliser of a basis of a t-dimensional subspace of 
$\mathbb{F}_q^n$. In case of equality, the characteristic vector of Y is a linear combination of the characteristic vectors of the cosets of these stabilisers. We also give similar results for subsets of 
$\text{GL}(n,q)$ that intersect not necessarily pointwise in t-dimensional subspaces of 
$\mathbb{F}_q^n$ and for cross-intersecting subsets of 
$\text{GL}(n,q)$. These results may be viewed as variants of the classical Erdős–Ko–Rado Theorem in extremal set theory and are q-analogs of corresponding results known for the symmetric group. Our methods are based on eigenvalue techniques to estimate the size of the largest independent sets in graphs and crucially involve the representation theory of 
$\text{GL}(n,q)$.
Index
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp 567-574
-
- Chapter
-
- You have access
- Open access
- Export citation
XIV - Weak interactions of heavy quarks
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp 399-433
-
- Chapter
-
- You have access
- Open access
- Export citation
14 - Mean field theory
-
- Book:
- Quarks, Gluons and Lattices
- Published online:
- 05 November 2022
- Print publication:
- 16 February 2023, pp 94-100
-
- Chapter
-
- You have access
- Open access
- Export citation
Contents
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp vii-xvi
-
- Chapter
-
- You have access
- Open access
- Export citation
4 - Scalar fields
-
- Book:
- Quarks, Gluons and Lattices
- Published online:
- 05 November 2022
- Print publication:
- 16 February 2023, pp 14-19
-
- Chapter
-
- You have access
- Open access
- Export citation
10 - Knot theory and physical states of quantum gravity
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp 238-274
-
- Chapter
-
- You have access
- Open access
- Export citation
IX - Mass mixing and CP violation
-
- Book:
- Dynamics of the Standard Model
- Published online:
- 04 November 2022
- Print publication:
- 16 February 2023, pp 260-277
-
- Chapter
-
- You have access
- Open access
- Export citation
7 - Quantum gravity
-
- Book:
- Loops, Knots, Gauge Theories and Quantum Gravity
- Published online:
- 10 November 2022
- Print publication:
- 16 February 2023, pp 161-187
-
- Chapter
-
- You have access
- Open access
- Export citation
1 - Quarks and gluons
-
- Book:
- Quarks, Gluons and Lattices
- Published online:
- 05 November 2022
- Print publication:
- 16 February 2023, pp 1-4
-
- Chapter
-
- You have access
- Open access
- Export citation
