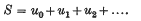Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The theory of queues with a single server
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-289
- Print publication:
- April 1952
-
- Article
- Export citation
Note on the foundations of projective geometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-364
- Print publication:
- April 1952
-
- Article
- Export citation
A method for the determination of converging factors, applied to the asymptotic expansions for the parabolic cylinder functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-254
- Print publication:
- April 1952
-
- Article
- Export citation
PSP volume 48 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1952
-
- Article
-
- You have access
- Export citation
Random motion on a finite abelian group - Corrigenda
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, p. 368
- Print publication:
- April 1952
-
- Article
-
- You have access
- Export citation
NAV volume 5 issue 2 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- April 1952
-
- Article
-
- You have access
- Export citation
PSP volume 48 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1952
-
- Article
-
- You have access
- Export citation
Sequential tests for composite hypotheses
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 290-299
- Print publication:
- April 1952
-
- Article
- Export citation
Selecting the Moon's Limb
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 141-146
- Print publication:
- April 1952
-
- Article
- Export citation
The Treatment of Navigational Errors
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 103-124
- Print publication:
- April 1952
-
- Article
- Export citation
Course and Distance Correction
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 18 January 2010, p. 202
- Print publication:
- April 1952
-
- Article
-
- You have access
- Export citation
The solution of algebraic equations on the EDSAC
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 2 / April 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-270
- Print publication:
- April 1952
-
- Article
- Export citation
Factorization of the algebra of particles of half-odd spin
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 110-117
- Print publication:
- January 1952
-
- Article
- Export citation
Some Recent Work on Polar Navigation
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 12-26
- Print publication:
- January 1952
-
- Article
- Export citation
The Hahn-Banach theorem for non-Archimedean-valued fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-45
- Print publication:
- January 1952
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 24 October 2008, p. 208
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
Fifth Annual General Meeting
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 84-94
- Print publication:
- January 1952
-
- Article
- Export citation
Navigation and the Shipping Industry
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 1-11
- Print publication:
- January 1952
-
- Article
- Export citation
The inhomogeneous minimum of binary quadratic, ternary cubic and quaternary quartic forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 48 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 24 October 2008, pp. 72-86
- Print publication:
- January 1952
-
- Article
- Export citation
Course and Distance Correction from an Estimated Position
-
- Journal:
- The Journal of Navigation / Volume 5 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 January 2010, pp. 39-41
- Print publication:
- January 1952
-
- Article
- Export citation