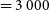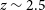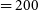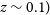Refine search
Actions for selected content:
28007 results in Astrophysics
10 - The Jeans Equations and the Tensor Virial Theorem
- from Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 172-196
-
- Chapter
- Export citation
9 - The Collisionless Boltzmann Equation and the Jeans Theorem
- from Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 151-171
-
- Chapter
- Export citation
Contents
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp v-viii
-
- Chapter
- Export citation
12 - Modeling Techniques 1: Phase-Space Approach
- from Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 211-235
-
- Chapter
- Export citation
3 - Tidal Fields
- from Part I - Potential Theory
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 49-69
-
- Chapter
- Export citation
Spectroscopic and photometric analysis of 21 chromospherically active variables: Activity cycles and differential rotation
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 38 / 2021
- Published online by Cambridge University Press:
- 10 June 2021, e027
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Part II - Systems of Particles
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 103-104
-
- Chapter
- Export citation
References
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 333-343
-
- Chapter
- Export citation
Part I - Potential Theory
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 1-2
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 344-348
-
- Chapter
- Export citation
14 - Modeling Techniques 3: From ρ to f
- from Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 281-295
-
- Chapter
- Export citation
6 - The N-Body Problem and the Virial Theorem
- from Part II - Systems of Particles
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 105-123
-
- Chapter
- Export citation
Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 149-150
-
- Chapter
- Export citation
4 - The Two-Body Problem
- from Part I - Potential Theory
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 70-82
-
- Chapter
- Export citation
Appendix - Mathematical Background
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 296-332
-
- Chapter
- Export citation
1 - The Gravitational Field
- from Part I - Potential Theory
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 3-13
-
- Chapter
- Export citation
Murchison Widefield Array rapid-response observations of the short GRB 180805A
- Part of
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 38 / 2021
- Published online by Cambridge University Press:
- 10 June 2021, e026
-
- Article
-
- You have access
- HTML
- Export citation
11 - Projected Dynamics
- from Part III - Collisionless Systems
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 197-210
-
- Chapter
- Export citation
7 - Relaxation 1: Two-Body Relaxation
- from Part II - Systems of Particles
-
- Book:
- Introduction to Stellar Dynamics
- Published online:
- 28 May 2021
- Print publication:
- 10 June 2021, pp 124-136
-
- Chapter
- Export citation