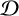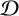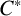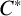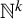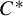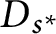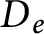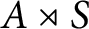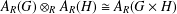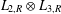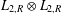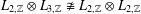Refine search
Actions for selected content:
26 results
Quasi-invariant lifts of completely positive maps for groupoid actions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 19 August 2025, pp. 35-63
- Print publication:
- January 2026
-
- Article
- Export citation
ÉTALE STRUCTURES AND THE JOYAL–TIERNEY REPRESENTATION THEOREM IN COUNTABLE MODEL THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 July 2025, pp. 1-52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The imprimitivity Fell bundle
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-44
-
- Article
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
Homology and K-theory of dynamical systems IV. Further structural results on groupoid homology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 May 2024, pp. 247-273
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON PROJECTIONS IN ÉTALE GROUPOID ALGEBRAS AND DIAGONAL-PRESERVING HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 508-513
- Print publication:
- December 2024
-
- Article
- Export citation
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
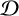 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
- Print publication:
- June 2024
-
- Article
- Export citation
A correspondence between inverse subsemigroups, open wide subgroupoids and cartan intermediate C*-subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 October 2022, pp. 861-879
-
- Article
- Export citation
A counterexample to the HK-conjecture that is principal
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1829-1846
- Print publication:
- June 2023
-
- Article
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
Cocycles on groupoids arising from
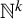 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTS, CROSSED PRODUCTS AND INVERSE SEMIGROUP COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 253-288
- Print publication:
- April 2023
-
- Article
- Export citation
INVARIANT SETS AND NORMAL SUBGROUPOIDS OF UNIVERSAL ÉTALE GROUPOIDS INDUCED BY CONGRUENCES OF INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 April 2021, pp. 99-118
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
Étale groupoid algebras with coefficients in a sheaf and skew inverse semigroup rings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 1592-1626
- Print publication:
- December 2021
-
- Article
- Export citation
QUOTIENTS OF ÉTALE GROUPOIDS AND THE ABELIANIZATIONS OF GROUPOID C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 07 April 2020, pp. 56-75
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
TENSOR PRODUCTS OF STEINBERG ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 111-126
- Print publication:
- August 2021
-
- Article
- Export citation
GCR and CCR Steinberg Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1581-1606
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation