Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T12:52:56.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Étale groupoid algebras with coefficients in a sheaf and skew inverse semigroup rings

Part of: Special categories Rings and algebras arising under various constructions Topological and differentiable algebraic systems Semigroups

Published online by Cambridge University Press:  07 August 2020

Daniel Gonçalves  and
Benjamin Steinberg
Daniel Gonçalves*
Affiliation:
Departmento de Matemática, Universidade Federal de Santa Catarina, Florianópolis, Brazil
Benjamin Steinberg
Affiliation:
Department of Mathematics, City College of New York, New York, NY, USA e-mail: bsteinberg@ccny.cuny.edu
*
e-mail: daemig@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an action 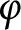${\varphi }$ of inverse semigroup S on a ring A (with domain of 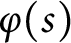${\varphi }(s)$ denoted by 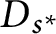$D_{s^*}$), we show that if the ideals 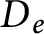$D_e$, with e an idempotent, are unital, then the skew inverse semigroup ring 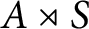$A\rtimes S$ can be realized as the convolution algebra of an ample groupoid with coefficients in a sheaf of (unital) rings. Conversely, we show that the convolution algebra of an ample groupoid with coefficients in a sheaf of rings is isomorphic to a skew inverse semigroup ring of this sort. We recover known results in the literature for Steinberg algebras over a field as special cases.

Keywords

Étale groupoidsinverse semigroupsrings

MSC classification

Primary: 22A22: Topological groupoids (including differentiable and Lie groupoids)
Secondary: 20M18: Inverse semigroups 18B40: Groupoids, semigroupoids, semigroups, groups (viewed as categories) 16S36: Ordinary and skew polynomial rings and semigroup rings

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 6 , December 2021 , pp. 1592 - 1626
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

B. S. thanks the Fulbright commission for its support in visiting the Federal University of Santa Catarina in Brazil and the PSC-CUNY. D. G. was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) grant numbers 304487/2017-1 and 406122/2018-0 and Capes-PrInt grant number 88881.310538/2018-01—Brazil.

References

Abrams, G., Ara, P., and Siles Molina, M., Leavitt path algebras. Lecture Notes in Mathematics, 2191, Springer, London, 2017.CrossRefGoogle Scholar
Ara, P., Bosa, J., Hazrat, R., and Sims, A., Reconstruction of graded groupoids from graded Steinberg algebras . Forum Math. 29(2017), no. 5, 1023–1037.CrossRefGoogle Scholar
Ara, P. and Goodearl, K. R., Leavitt path algebras of separated graphs . J. Reine Angew. Math. 2012(2012), no. 669, 165–224.CrossRefGoogle Scholar
Beuter, V., Partial actions of inverse semigroups and their associated algebras. Ph.D. thesis, Universidade Federal de Santa Catarina, 2018. http://ppgmtm.posgrad.ufsc.br/files/2017/09/Tese_Viviane.pdfGoogle Scholar
Beuter, V. and Cordeiro, L. G., The dynamics of partial inverse semigroup actions . J. Pure Appl. Algebra 224(2020), no. 3, 917–957.Google Scholar
Beuter, V. and Gonçalves, D., The interplay between Steinberg algebras and skew rings . J. Algebra 497(2018), 337–362.CrossRefGoogle Scholar
Beuter, V., Gonçalves, D., Öinert, J., and Royer, D., Simplicity of skew inverse semigroups with applications to Steinberg algebras and topological dynamics . Forum Math. 31(2019), 543–562.CrossRefGoogle Scholar
Brown, J., Clark, L. O., Farthing, C., and Sims, A., Simplicity of algebras associated to étale groupoids . Semigroup Forum 88(2014), no. 2, 433–452.CrossRefGoogle Scholar
Bourbaki, N., General topology: chapters 5–10. Springer-Verlag, Berlin, Heidelberg, 1998.Google Scholar
Buss, A. and Exel, R., Inverse semigroup expansions and their actions on ${C}^{\ast }$ -algebras . Illinois J. Math. 56(2012), no. 4, 1185–1212.CrossRefGoogle Scholar
Carlsen, T. M. and Rout, J., Diagonal-preserving graded isomorphisms of Steinberg algebras . Commun. Contemp. Math. 20(2018), no. 6, 1750064.CrossRefGoogle Scholar
Clark, L. O., Edie-Michell, C., an Huef, A., and Sims, A., Ideals of Steinberg algebras of strongly effective groupoids, with applications to Leavitt path algebras . Trans. Amer. Math. Soc. 371(2019), 5461–548.CrossRefGoogle Scholar
Clark, L. O. and Pangalela, Y. E. P., Kumjian–Pask algebras of finitely-alighed higher-rank graphs . J. Algebra 482(2017), 364–397.CrossRefGoogle Scholar
Clark, L. O., Steinberg, B., and van Wyk, D. W., GCR and CCR Steinberg algebras. Canad. J. Math., to appear. http://dx.doi.org/10.4153/S0008414X19000415CrossRefGoogle Scholar
Cordeiro, L., Soficity and other dynamical aspects of groupoids and inverse semigroups. Ph.D. thesis, University of Ottawa, Ottawa, 2018. http://dx.doi.org/10.20381/ruor-22277CrossRefGoogle Scholar
Demeneghi, P., The ideal structure of Steinberg algebras . Adv. Math. 352(2019), 777–835.CrossRefGoogle Scholar
Dowker, C. H., Lectures on sheaf theory. Tata Institute of Fundamental Research, Bombay, 1956. Notes by S. V. Adavi and N. Ramabhadran.Google Scholar
Exel, R., Inverse semigroups and combinatorial ${C}^{\ast }$ -algebras . Bull. Braz. Math. Soc. (N.S.) 39(2008), no. 2, 191–313.CrossRefGoogle Scholar
Gonçalves, D. and Royer, D., Leavitt path algebras as partial skew group rings . Comm. Algebra 42(2014), 3578–3592.CrossRefGoogle Scholar
Gonçalves, D. and Royer, D., Simplicity and chain conditions for ultragraph Leavitt path algebras via partial skew group ring theory . J. Aust. Math. Soc., to appear. http://dx.doi.org/10.1017/S144678871900020X CrossRefGoogle Scholar
Hazrat, R. and Li, H., Graded Steinberg algebras and partial actions . J. Pure Appl. Algebra 22(2018), no. 12, 3946–3967.CrossRefGoogle Scholar
Howie, J. M., An introduction to semigroup theory. Academic Press, London, New York, 1976.Google Scholar
Lawson, M. V., Inverse semigroups—the theory of partial symmetries. World Scientific Publishing Co. Inc., River Edge, NJ, 1998.CrossRefGoogle Scholar
Nystedt, P., Simplicity of algebras via epsilon-strong systems. Colloq. Math. 162(2020), 279–301. http://dx.doi.org/10.4064/cm7887-9-2019 CrossRefGoogle Scholar
Nystedt, P., Öinert, J., and Pinedo, H., Artinian and noetherian partial skew groupoid rings . J. Algebra 503(2018), 433–452.CrossRefGoogle Scholar
Pierce, R. S., Modules over commutative regular rings. Memoirs of the American Mathematical Society, 70, American Mathematical Society, Providence, RI, 1967.CrossRefGoogle Scholar
Renault, J., Représentation des produits croisés d’algèbres de groupoïdes . J. Operator Theory 18(1987), no. 1, 67–97.Google Scholar
Steinberg, B., A groupoid approach to discrete inverse semigroup algebras. Preprint, 2009. arXiv:0903.3456Google Scholar
Steinberg, B., A groupoid approach to discrete inverse semigroup algebras . Adv. Math. 223(2010), no. 2, 689–727.CrossRefGoogle Scholar
Steinberg, B., Modules over étale groupoid algebras as sheaves . J. Aust. Math. Soc. 97(2014), no. 3, 418–429.CrossRefGoogle Scholar
Steinberg, B., Simplicity, primitivity and semiprimitivity of étale groupoid algebras with applications to inverse semigroup algebras . J. Pure Appl. Algebra 220(2016), no. 3, 1035–1054.CrossRefGoogle Scholar
Steinberg, B., Ideals of étale groupoid algebras and Exel’s Effros-Hahn conjecture. J. Noncommut. Geom. Preprint, 2018. arXiv:1810.10580v2Google Scholar