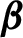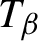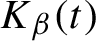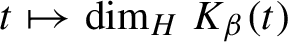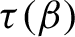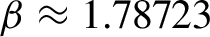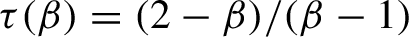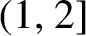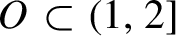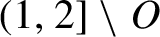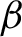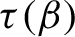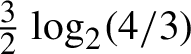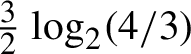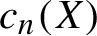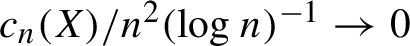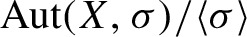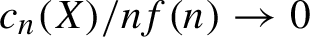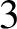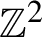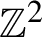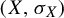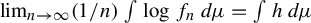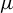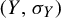Contents
Original Article
Critical values for the
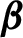 $\boldsymbol{\beta} $-transformation with a hole at
$\boldsymbol{\beta} $-transformation with a hole at 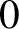 $0$
$0$
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1785-1828
-
- Article
- Export citation
A counterexample to the HK-conjecture that is principal
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1829-1846
-
- Article
- Export citation
A complete proof that square ice entropy is
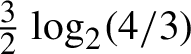 $\tfrac 32\log _{2} (4/3)$
$\tfrac 32\log _{2} (4/3)$
- Part of:
-
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1847-1908
-
- Article
- Export citation
Regularity of calibrated sub-actions for circle expanding maps and Sturmian optimization
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2022, pp. 1909-1921
-
- Article
- Export citation
Direct prime subshifts and canonical covers
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2022, pp. 1922-1941
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bowen–Walters expansiveness for semigroups of linear operators
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1942-1951
-
- Article
- Export citation
Disjointness for measurably distal group actions and applications
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2022, pp. 1952-1979
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local finiteness and automorphism groups of low complexity subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1980-2001
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper
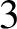 $3$-colorings of
$3$-colorings of 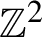 $\mathbb {Z}^{2}$ are Bernoulli
$\mathbb {Z}^{2}$ are Bernoulli
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2022, pp. 2002-2027
-
- Article
- Export citation
Geometric and combinatorial properties of self-similar multifractal measures
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2022, pp. 2028-2072
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relative f-invariant and non-uniform random sofic approximations
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2073-2110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative pressure functions and their equilibrium states
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2022, pp. 2111-2136
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 43 issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 May 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 43 issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 May 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation