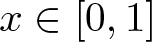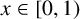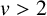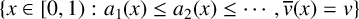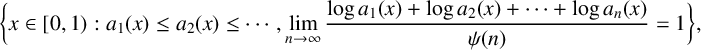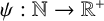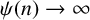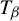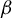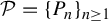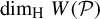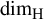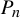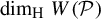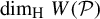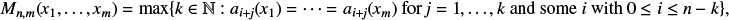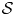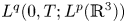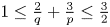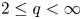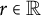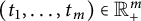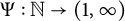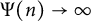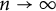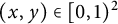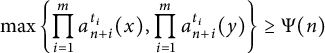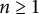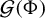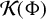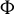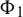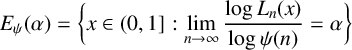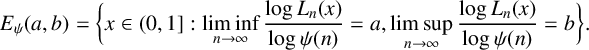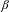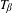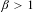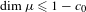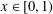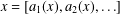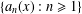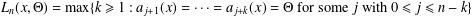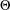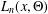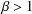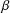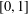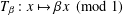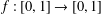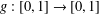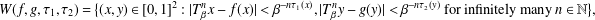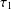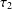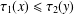Refine search
Actions for selected content:
34 results
METRICAL PROPERTIES OF CONTINUED FRACTION AND LÜROTH SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-35
-
- Article
- Export citation
Zero-full law for well approximable sets in missing digit sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 81-102
- Print publication:
- January 2025
-
- Article
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MULTIFRACTAL SPECTRUM OF CONTINUED FRACTIONS WITH NONDECREASING PARTIAL QUOTIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 93-105
- Print publication:
- August 2025
-
- Article
- Export citation
Shrinking parallelepiped targets for
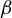 $\beta $-dynamical systems
$\beta $-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 1827-1842
- Print publication:
- June 2025
-
- Article
- Export citation
Uniform Diophantine approximation and run-length function in continued fractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1246-1280
- Print publication:
- April 2025
-
- Article
- Export citation
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 186-195
- Print publication:
- April 2024
-
- Article
- Export citation
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 727-745
- Print publication:
- June 2024
-
- Article
- Export citation
A note on the relative growth of products of multiple partial quotients in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 544-552
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2707-2731
- Print publication:
- August 2023
-
- Article
- Export citation
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
- Print publication:
- April 2023
-
- Article
- Export citation
HIGHER-DIMENSIONAL SHRINKING TARGET PROBLEM FOR BETA DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 289-311
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractal projections with an application in number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1760-1784
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of the set of almost convergent sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 691-697
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
- Print publication:
- June 2022
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
Maximizing Bernoulli measures and dimension gaps for countable branched systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1921-1939
- Print publication:
- July 2021
-
- Article
- Export citation
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 196-206
- Print publication:
- October 2020
-
- Article
- Export citation
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 186-195
- Print publication:
- October 2020
-
- Article
- Export citation