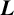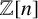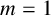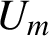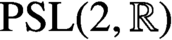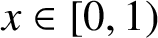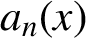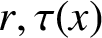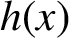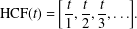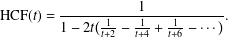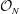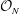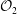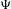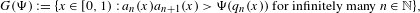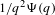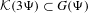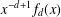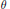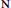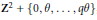Refine search
Actions for selected content:
28 results
A new class of α-Farey maps and an application to normal numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
METRICAL PROPERTIES OF CONTINUED FRACTION AND LÜROTH SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
On congruence subgroups generated by two parabolic rational matrices
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-20
-
- Article
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-35
-
- Article
- Export citation
TRANSCENDENTAL RUBAN p-ADIC CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 80-92
- Print publication:
- August 2025
-
- Article
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 439-447
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR DIRECTIONS IN VEECH SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2022, pp. 390-397
- Print publication:
- June 2023
-
- Article
- Export citation
APÉRY LIMITS FOR ELLIPTIC
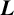 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
- Print publication:
- December 2022
-
- Article
- Export citation
ON TRANSCENDENTAL CONTINUED FRACTIONS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 392-403
- Print publication:
- June 2022
-
- Article
- Export citation
ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 45-58
- Print publication:
- August 2021
-
- Article
- Export citation
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2020, pp. 1-29
- Print publication:
- February 2022
-
- Article
- Export citation
AN EXACT FORMULA FOR THE HARMONIC CONTINUED FRACTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 11-21
- Print publication:
- February 2021
-
- Article
- Export citation
Slow Continued Fractions and Permutative Representations of
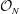 ${\mathcal{O}}_{N}$
${\mathcal{O}}_{N}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 January 2020, pp. 787-801
- Print publication:
- December 2020
-
- Article
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
- Print publication:
- December 2020
-
- Article
- Export citation
ON GENERALIZED THUE–MORSE FUNCTIONS AND THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 177-201
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Diophantine Approximation for CertainAlgebraic Formal Power Series in PositiveCharacteristic
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-683
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
SOME EXACT ALGEBRAIC EXPRESSIONS FOR THE TAILS OF TASOEV CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 179-193
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Continued fractions with low complexity: transcendence measures and quadratic approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 718-750
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Cyclic Groups and the Three Distance Theorem
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 3 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-552
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation