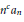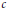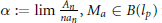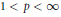Refine search
Actions for selected content:
3 results
BOUNDS FOR THE DEVIATION OF A FUNCTION FROM THE CHORD GENERATED BY ITS EXTREMITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 225-248
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Weighted Mean Operators on lp
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 4 / 01 December 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 406-412
- Print publication:
- 01 December 2000
-
- Article
-
- You have access
- Export citation
-
Abstract. The weighted mean matrix
${{M}_{a}}$ is the triangular matrix 
$\left\{ {{a}_{k}}/{{A}_{n}} \right\}$ , where 
${{a}_{n}}\,>\,0$ and 
${{A}_{n}}\,:=\,{{a}_{1}}\,+\,{{a}_{2}}\,+\cdots +\,{{a}_{n}}$ . It is proved that, subject to 
${{n}^{c}}{{a}_{n}}$ being eventually monotonic for each constant 
$c$ and to the existence of 
$\alpha \,:=\,\lim \,\frac{{{A}_{n}}}{n{{a}_{n}}},\,{{M}_{a}}\,\in \,B\left( {{l}_{p}} \right)$ for 
$1\,<\,p\,<\infty $ if and only if 
$\alpha \,<\,p$ .
Simple Conditions for Matrices to be Bounded Operators on lp
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 10-14
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
-
The two theorems proved yield simple yet reasonably general conditions for triangular matrices to be bounded operators on
${{l}_{p}}$ . The theorems are applied to Nörlund and weighted mean matrices.
