Refine search
Actions for selected content:
3 results
ORDER BOUNDED WEIGHTED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 09 April 2013, pp. 333-343
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS BETWEEN WEIGHTED BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Essential Norm and Weak Compactness of Composition Operators on Weighted Banach Spaces of Analytic Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-148
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation
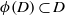
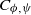
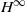
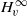 or
or