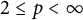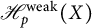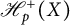Refine search
Actions for selected content:
4 results
Volterra operators between Hardy spaces of vector-valued Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 286-300
- Print publication:
- March 2025
-
- Article
- Export citation
26 - Bohr’s Problem for Vector-Valued Dirichlet Series
- from Part 4 - Vector-Valued Aspects
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 645-663
-
- Chapter
- Export citation
24 - Vector-Valued Hardy Spaces
- from Part 4 - Vector-Valued Aspects
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 584-611
-
- Chapter
- Export citation
11 - Hardy Spaces of Dirichlet Series
- from Part 1 - Bohr’s Problem and Complex Analysis on Polydiscs
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 268-288
-
- Chapter
- Export citation