Refine search
Actions for selected content:
15 results
Equivariant vector bundles on toric schemes over semirings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSION OF COHOMOLOGY CLASSES FOR VECTOR BUNDLES WITH SINGULAR HERMITIAN METRICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 562-580
- Print publication:
- September 2025
-
- Article
- Export citation
9 - Fano Threefolds
-
- Book:
- Complex Algebraic Threefolds
- Published online:
- 29 September 2023
- Print publication:
- 19 October 2023, pp 359-409
-
- Chapter
- Export citation
Reconstruction of topological graphs and their Hilbert bimodules
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 October 2023, pp. 514-539
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some results on extension of maps and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1465-1472
- Print publication:
- December 2019
-
- Article
- Export citation
ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 195-202
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Projective Plane Bundles Over an Elliptic Curve
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 201-210
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
Stability of Vector Bundles on Curves and Degenerations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 858-864
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
RANK TWO STABLE ULRICH BUNDLES ON ANTICANONICALLY EMBEDDED SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 22-37
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
The Fixed Point Locus of the Verschiebung on ℳX(2, 0) for Genus-2 Curves X in Charateristic 2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-448
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
On derivations and elementary operators on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 515-534
-
- Article
-
- You have access
- Export citation
On a gauge-invariant functional
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 143-151
-
- Article
-
- You have access
- Export citation
VECTOR BUNDLES OVER A NONDEGENERATE CONIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 145-154
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A Compactness Theorem for Yang-Mills Connections
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 4 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 624-634
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
Local Systems on $\mathbb P$1 − S for S a Finite Set
-
- Journal:
- Compositio Mathematica / Volume 129 / Issue 1 / October 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 67-86
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation



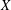
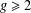
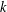
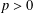

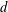
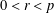

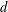
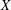
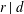
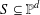
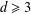
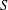
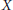

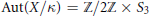
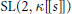
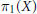
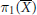
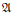 over the maximal ideal space of the centre of
over the maximal ideal space of the centre of