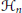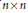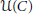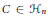Refine search
Actions for selected content:
1 results
Some Convexity Features Associated with Unitary Orbits
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 1 / 01 February 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 91-111
- Print publication:
- 01 February 2003
-
- Article
-
- You have access
- Export citation