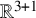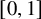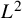Refine search
Actions for selected content:
1 results
The zero mass problem for Klein-Gordon equations: quadratic null interactions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation