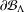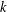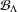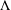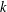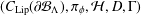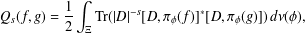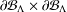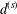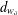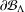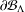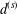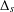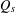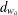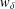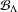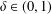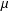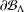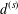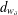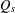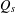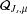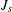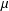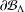Refine search
Actions for selected content:
1 results
DIRICHLET FORMS AND ULTRAMETRIC CANTOR SETS ASSOCIATED TO HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 194-219
- Print publication:
- April 2021
-
- Article
- Export citation
-
The aim of this paper is to study the heat kernel and the jump kernel of the Dirichlet form associated to the ultrametric Cantor set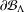
$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ that is the infinite path space of the stationary 
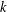$k$-Bratteli diagram 
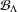${\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, where 
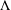$\unicode[STIX]{x1D6EC}$ is a finite strongly connected 
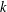$k$-graph. The Dirichlet form which we are interested in is induced by an even spectral triple 
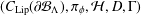$(C_{\operatorname{Lip}}(\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}),\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}},{\mathcal{H}},D,\unicode[STIX]{x1D6E4})$ and is given by where
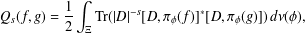$$\begin{eqnarray}Q_{s}(f,g)=\frac{1}{2}\int _{\unicode[STIX]{x1D6EF}}\operatorname{Tr}(|D|^{-s}[D,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}}(f)]^{\ast }[D,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}}(g)])\,d\unicode[STIX]{x1D708}(\unicode[STIX]{x1D719}),\end{eqnarray}$$
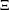$\unicode[STIX]{x1D6EF}$ is the space of choice functions on 
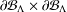$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}\times \unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$. There are two ultrametrics, 
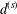$d^{(s)}$ and 
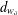$d_{w_{\unicode[STIX]{x1D6FF}}}$, on 
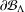$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ which make the infinite path space 
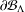$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ an ultrametric Cantor set. The former 
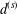$d^{(s)}$ is associated to the eigenvalues of the Laplace–Beltrami operator 
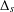$\unicode[STIX]{x1D6E5}_{s}$ associated to 
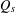$Q_{s}$, and the latter 
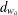$d_{w_{\unicode[STIX]{x1D6FF}}}$ is associated to a weight function 
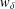$w_{\unicode[STIX]{x1D6FF}}$ on 
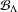${\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, where 
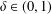$\unicode[STIX]{x1D6FF}\in (0,1)$. We show that the Perron–Frobenius measure 
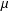$\unicode[STIX]{x1D707}$ on 
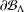$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ has the volume-doubling property with respect to both 
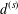$d^{(s)}$ and 
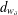$d_{w_{\unicode[STIX]{x1D6FF}}}$ and we study the asymptotic behavior of the heat kernel associated to 
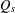$Q_{s}$. Moreover, we show that the Dirichlet form 
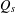$Q_{s}$ coincides with a Dirichlet form 
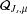${\mathcal{Q}}_{J_{s},\unicode[STIX]{x1D707}}$ which is associated to a jump kernel 
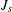$J_{s}$ and the measure 
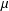$\unicode[STIX]{x1D707}$ on 
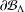$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, and we investigate the asymptotic behavior and moments of displacements of the process.
