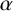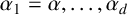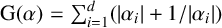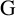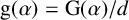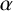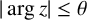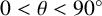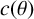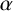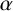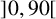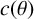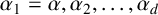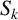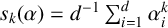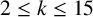Refine search
Actions for selected content:
3 results
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
- Print publication:
- April 2023
-
- Article
- Export citation
THE ABSOLUTE
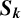 $\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
- Print publication:
- April 2023
-
- Article
- Export citation
THE TRACE PROBLEM FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 17 February 2011, pp. 341-354
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation