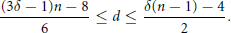Refine search
Actions for selected content:
2 results
A NOTE ON GROUP RINGS WITH TRIVIAL UNITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 19 July 2021, pp. 243-247
- Print publication:
- April 2022
-
- Article
- Export citation
3-torsion in the Homology of Complexes ofGraphs of Bounded Degree
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 843-862
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation