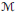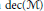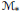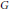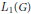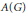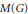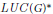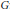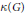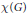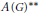Let G be a locally compact group and H be a compact subgroup of G. Using a general criterion established by Neufang [‘A unified approach to the topological centre problem for certain Banach algebras arising in abstract harmonic analysis’, Arch. Math.82(2) (2004), 164–171], we show that the Banach algebra L1(G/H) is strongly Arens irregular for a large class of locally compact groups.

In this paper, a general construction of a skew-product dynamical system, for which the skew-product dynamical system studied by Hahn is a special case, is given. Then the ergodic and topological properties (of a special type) of our newly defined systems (called Milnes-type systems) are investigated. It is shown that the Milnes-type systems are actually natural extensions of dynamical systems corresponding to some special distal functions. Finally, the topological centre of Ellis groups of any skew-product dynamical system is calculated.

The decomposability number of a von Neumann algebra 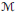\mathcal{M}$\mathcal{M}$ (denoted by 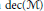\text{dec}\left( \mathcal{M} \right)$\text{dec}\left( \mathcal{M} \right)$) is the greatest cardinality of a family of pairwise orthogonal non-zero projections in 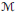\mathcal{M}$\mathcal{M}$. In this paper, we explore the close connection between 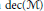\text{dec}\left( \mathcal{M} \right)$\text{dec}\left( \mathcal{M} \right)$ and the cardinal level of the Mazur property for the predual 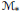{{\mathcal{M}}_{*}}${{\mathcal{M}}_{*}}$ of 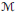\mathcal{M}$\mathcal{M}$, the study of which was initiated by the second author. Here, our main focus is on those von Neumann algebras whose preduals constitute such important Banach algebras on a locally compact group 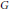G$G$ as the group algebra 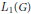{{L}_{1}}(G)${{L}_{1}}(G)$, the Fourier algebra 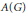A(G)$A(G)$, the measure algebra 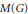M(G)$M(G)$, the algebra 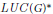LUC{{(G)}^{*}}$LUC{{(G)}^{*}}$, etc. We show that for any of these von Neumann algebras, say 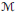\mathcal{M}$\mathcal{M}$, the cardinal number dec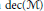(\mathcal{M})$(\mathcal{M})$ and a certain cardinal level of the Mazur property of 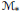{{\mathcal{M}}_{*}}${{\mathcal{M}}_{*}}$ are completely encoded in the underlying group structure. In fact, they can be expressed precisely by two dual cardinal invariants of 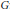G$G$: the compact covering number 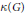\kappa (G)$\kappa (G)$ of 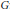G$G$ and the least cardinality 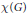\mathcal{X}(G)$\mathcal{X}(G)$ of an open basis at the identity of 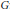G$G$. We also present an application of the Mazur property of higher level to the topological centre problem for the Banach algebra 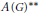A{{(G)}^{**}}$A{{(G)}^{**}}$.