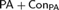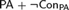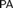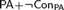Refine search
Actions for selected content:
1 results
UNIVERSAL ROSSER PREDICATES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 292-302
- Print publication:
- March 2017
-
- Article
- Export citation