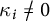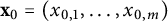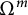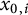Refine search
Actions for selected content:
1 results
Existence of stationary vortex sheets for the 2D incompressible Euler equation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 828-853
- Print publication:
- June 2023
-
- Article
- Export citation
-
We construct a new type of planar Euler flows with localized vorticity. Let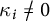
$\kappa _i\not =0$, 
$i=1,\ldots , m$, be m arbitrarily fixed constants. For any given nondegenerate critical point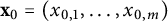 
$\mathbf {x}_0=(x_{0,1},\ldots ,x_{0,m})$ of the Kirchhoff–Routh function defined on 
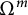$\Omega ^m$ corresponding to 
$(\kappa _1,\ldots , \kappa _m)$, we construct a family of stationary planar flows with vortex sheets that have large vorticity amplitude and concentrate on curves perturbed from small circles centered near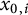 
$x_{0,i}$, 
$i=1,\ldots ,m$. The proof is accomplished via the implicit function theorem with suitable choice of function spaces.
