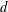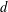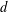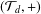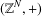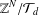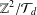Refine search
Actions for selected content:
1 results
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation