Refine search
Actions for selected content:
3 results
ON BAD SUPERNILPOTENT RADICALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 15 December 2011, pp. 271-274
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON SUPERNILPOTENT NONSPECIAL RADICALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 107-110
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
On special radicals, supernilpotent radicals and weakly homomorphically closed classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 152-162
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
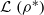 be the lower radical determined by
be the lower radical determined by 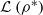 is a supernilpotent radical with
is a supernilpotent radical with 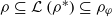 and they asked whether
and they asked whether  if
if 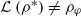 . We recall that a prime ring
. We recall that a prime ring  .
.