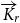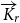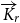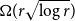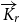Refine search
Actions for selected content:
1 results
Strong complete minors in digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 24 September 2021, pp. 489-506
-
- Article
- Export citation