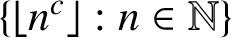Refine search
Actions for selected content:
1 results
CONSECUTIVE SQUARE-FREE NUMBERS IN PIATETSKI-SHAPIRO SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 217-222
- Print publication:
- April 2022
-
- Article
- Export citation