Refine search
Actions for selected content:
4 results
1 - The Origins of Operator-Theoretic Approaches to Function Theory
- from PART ONE - Commutative Theory
-
- Book:
- Operator Analysis
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 3-32
-
- Chapter
- Export citation

Operator Analysis
- Hilbert Space Methods in Complex Analysis
-
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020
Operators having the symmetrized bidisc as a spectral set
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 195-210
-
- Article
-
- You have access
- Export citation
Von Neumann Operators in
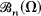
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 2 / 01 June 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 146-156
- Print publication:
- 01 June 1984
-
- Article
-
- You have access
- Export citation
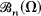
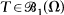 , is a spectral set for
, is a spectral set for 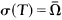 , then σ(
, then σ( with
with 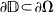 .
.