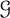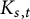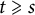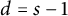Refine search
Actions for selected content:
20 results
Cyber breach risk modeling for insurance: capturing temporal and cross-group dependence
-
- Journal:
- Annals of Actuarial Science , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximated Penalized Maximum Likelihood for Exploratory Factor Analysis: An Orthogonal Case
-
- Journal:
- Psychometrika / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 01 January 2025, pp. 628-649
-
- Article
- Export citation
16 - Sampling Based on Sparsity*
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 626-637
-
- Chapter
- Export citation
Multitask feature selection within structural datasets
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 07 March 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On sparsity, power-law, and clustering properties of graphex processes - ADDENDUM
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 27 October 2023, p. 1
-
- Article
- Export citation
On sparsity, power-law, and clustering properties of graphex processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 1211-1253
- Print publication:
- December 2023
-
- Article
- Export citation
Exact recovery of Granger causality graphs with unconditional pairwise tests
-
- Journal:
- Network Science / Volume 11 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 431-457
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
12 - Local Structure and Nonuniform Recovery
- from PART III - Compressed Sensing with Local Structure
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 267-304
-
- Chapter
- Export citation
5 - An Introduction to Conventional Compressed Sensing
- from Part II - Compressed Sensing, Optimization and Wavelets
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 105-128
-
- Chapter
- Export citation
13 - Local Structure and Uniform Recovery
- from PART III - Compressed Sensing with Local Structure
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 305-333
-
- Chapter
- Export citation
Tree densities in sparse graph classes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1385-1404
- Print publication:
- October 2022
-
- Article
- Export citation
6 - Uncertainty Relations and Sparse Signal Recovery
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 163-196
-
- Chapter
- Export citation
14 - A Sparse Representation Approach for Anomaly Identification
- from Part IV - Signal Processing
-
-
- Book:
- Advanced Data Analytics for Power Systems
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 340-360
-
- Chapter
- Export citation
5 - Operator-Adapted Wavelets
- from Part I - The Sobolev Space Setting
-
- Book:
- Operator-Adapted Wavelets, Fast Solvers, and Numerical Homogenization
- Published online:
- 10 October 2019
- Print publication:
- 24 October 2019, pp 63-89
-
- Chapter
- Export citation
10 - Sharpening Spectrograms
- from Part II - Geometry and Statistics
-
- Book:
- Explorations in Time-Frequency Analysis
- Published online:
- 22 August 2018
- Print publication:
- 06 September 2018, pp 77-97
-
- Chapter
- Export citation
Properties of Discrete Framelet Transforms
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 18-47
- Print publication:
- 2013
-
- Article
- Export citation
On Generating Optimal Sparse Probabilistic Boolean Networks with Maximum Entropy from a Positive Stationary Distribution
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 2 / Issue 4 / November 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 353-372
- Print publication:
- November 2012
-
- Article
- Export citation
On Construction of Sparse Probabilistic Boolean Networks
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 2 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 1-18
- Print publication:
- February 2012
-
- Article
- Export citation
Convergence and regularization resultsfor optimal control problems with sparsity functional
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 858-886
- Print publication:
- July 2011
-
- Article
- Export citation
Coherent sources separation based on sparsity: an application to SSR signals
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 1 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 15 May 2009, pp. 185-191
-
- Article
- Export citation