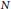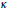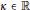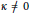Refine search
Actions for selected content:
2 results
The Classical N-body Problem in the Context of Curved Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 790-806
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
Continuous Hahn Polynomials of Differential Operator Argument and Analysis on Riemannian Symmetric Spaces of Constant Curvature
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 4 / 01 August 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-773
- Print publication:
- 01 August 1992
-
- Article
-
- You have access
- Export citation