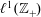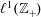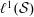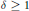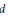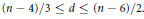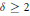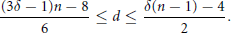Refine search
Actions for selected content:
2 results
Simplicial (Co)-homology of
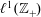 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 756-766
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
3-torsion in the Homology of Complexes ofGraphs of Bounded Degree
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 843-862
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation