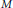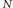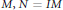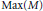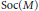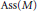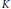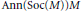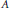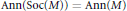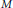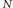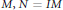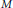An $R$ -module $M$ is called a multiplication module if for each submodule $N$ of $M,\,N\,=\,IM$ for some ideal $I$ of $R$ . As defined for a commutative ring $R$ , an $R$ -module $M$ is said to be semiprimitive if the intersection of maximal submodules of 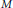$M$ is zero. The maximal spectra of a semiprimitive multiplication module 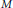$M$ are studied. The isolated points of 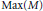$\text{Max}\left( M \right)$ are characterized algebraically. The relationships among the maximal spectra of 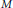$M$ , 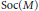$\text{Soc}\left( M \right)$ and 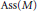$\text{Ass}\left( M \right)$ are studied. It is shown that 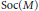$\text{Soc}\left( M \right)$ is exactly the set of all elements of 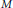$M$ which belongs to every maximal submodule of 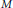$M$ except for a finite number. If 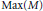$\text{Max}\left( M \right)$ is infinite, 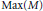$\text{Max}\left( M \right)$ is a one-point compactification of a discrete space if and only if 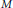$M$ is Gelfand and for some maximal submodule 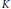$K$ , 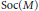$\text{Soc}\left( M \right)$ is the intersection of all prime submodules of 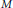$M$ contained in 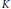$K$ . When 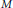$M$ is a semiprimitive Gelfand module, we prove that every intersection of essential submodules of 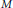$M$ is an essential submodule if and only if 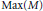$\text{Max}\left( M \right)$ is an almost discrete space. The set of uniform submodules of 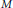$M$ and the set of minimal submodules of 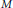$M$ coincide. 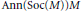$\text{Ann}\left( \text{Soc}\left( M \right) \right)M$ is a summand submodule of 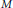$M$ if and only if 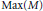$\text{Max}\left( M \right)$ is the union of two disjoint open subspaces 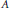$A$ and 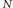$N$ , where 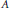$A$ is almost discrete and 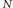$N$ is dense in itself. In particular, 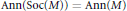$\text{Ann}\left( \text{Soc}\left( M \right) \right)\,=\,\text{Ann}\left( M \right)$ if and only if 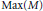$\text{Max}\left( M \right)$ is almost discrete.