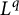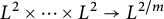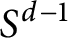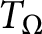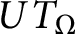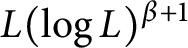Refine search
Actions for selected content:
2 results
On pointwise a.e. convergence of multilinear operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1005-1032
- Print publication:
- June 2024
-
- Article
- Export citation
An estimate for the composition of rough singular integral operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 911-922
- Print publication:
- December 2021
-
- Article
- Export citation