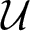We are interested in the optimal growth in terms of Lp-averages of hypercyclic and $\mathcal{U}$-frequently hypercyclic functions for some weighted Taylor shift operators acting on the space of analytic functions on the unit disc. We unify the results obtained by considering intermediate notions of upper frequent hypercyclicity between $\mathcal{U}$-frequent hypercyclicity and hypercyclicity.

In this paper we study the asymptotic behaviour near extinction of (sub-)critical continuous-state branching processes. In particular, we establish an analogue of Khintchine's law of the iterated logarithm near extinction time for a continuous-state branching process whose branching mechanism satisfies a given condition.

We study the rate of growth of entire functions that are frequently hypercyclic for the differentiation operator or the translation operator. Moreover, we prove the existence of frequently hypercyclic harmonic functions for the translation operator and we study the rate of growth of harmonic functions that are frequently hypercyclic for partial differentiation operators.

We investigate the asymptotic behaviour of homogeneous multidimensional Markov chains whose states have nonnegative integer components. We obtain growth rates for these models in a situation similar to the near-critical case for branching processes, provided that they converge to infinity with positive probability. Finally, the general theoretical results are applied to a class of controlled multitype branching process in which random control is allowed.