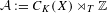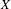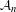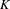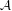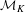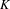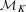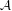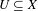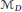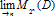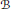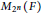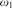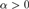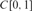Refine search
Actions for selected content:
3 results
Sylvester matrix rank functions on crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 2913-2946
- Print publication:
- November 2020
-
- Article
- Export citation
Uniqueness of the von Neumann Continuous Factor
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-982
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
A LIGHTFACE ANALYSIS OF THE DIFFERENTIABILITY RANK
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 240-265
- Print publication:
- March 2014
-
- Article
- Export citation