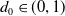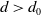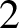Refine search
Actions for selected content:
3 results
Property (T) in k-gonal random groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 734-738
- Print publication:
- September 2022
-
- Article
- Export citation
Topology of random
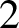 $2$-dimensional cubical complexes
$2$-dimensional cubical complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Briefing and debriefing: group psychological interventions in acute stressor situations
- from Part I - Key conceptual framework of debriefing
-
-
- Book:
- Psychological Debriefing
- Published online:
- 06 January 2010
- Print publication:
- 12 October 2000, pp 43-57
-
- Chapter
- Export citation