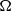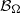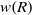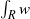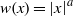Refine search
Actions for selected content:
1 results
DIRECTIONAL MAXIMAL OPERATORS AND RADIAL WEIGHTS ON THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 397-414
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation