Refine search
Actions for selected content:
2 results
Low Growth Equational Complexity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 197-210
-
- Article
- Export citation
Minimal varieties and quasivarieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-147
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
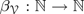
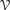 bounds the size of equation required to determine the membership of
bounds the size of equation required to determine the membership of 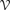 . Known examples of finitely generated varieties
. Known examples of finitely generated varieties 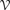 with unbounded equational complexity have growth in Ω(
with unbounded equational complexity have growth in Ω(