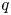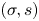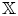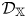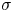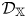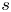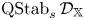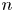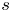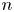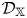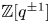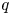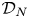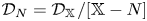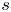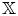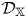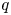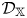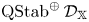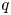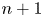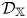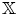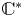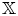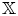We introduce 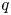 $q$-stability conditions
$q$-stability conditions 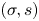 $(\sigma,s)$ on Calabi–Yau-
$(\sigma,s)$ on Calabi–Yau-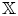 $\mathbb {X}$ categories
$\mathbb {X}$ categories 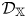 $\mathcal {D}_\mathbb {X}$, where
$\mathcal {D}_\mathbb {X}$, where 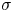 $\sigma$ is a stability condition on
$\sigma$ is a stability condition on 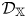 $\mathcal {D}_\mathbb {X}$ and
$\mathcal {D}_\mathbb {X}$ and 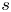 $s$ a complex number. We prove the corresponding deformation theorem, that
$s$ a complex number. We prove the corresponding deformation theorem, that 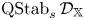 $\operatorname {QStab}_s\mathcal {D}_\mathbb {X}$ is a complex manifold of dimension
$\operatorname {QStab}_s\mathcal {D}_\mathbb {X}$ is a complex manifold of dimension 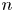 $n$ for fixed
$n$ for fixed 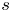 $s$, where
$s$, where 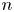 $n$ is the rank of the Grothendieck group of
$n$ is the rank of the Grothendieck group of 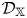 $\mathcal {D}_\mathbb {X}$ over
$\mathcal {D}_\mathbb {X}$ over 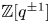 $\mathbb {Z}[q^{\pm 1}]$. When
$\mathbb {Z}[q^{\pm 1}]$. When  $s=N$ is an integer, we show that
$s=N$ is an integer, we show that 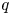 $q$-stability conditions can be identified with the stability conditions on
$q$-stability conditions can be identified with the stability conditions on 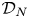 $\mathcal {D}_N$, provided the orbit category
$\mathcal {D}_N$, provided the orbit category 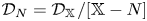 $\mathcal {D}_N=\mathcal {D}_\mathbb {X}/[\mathbb {X}-N]$ is well defined. To attack the questions on existence and deformation along the
$\mathcal {D}_N=\mathcal {D}_\mathbb {X}/[\mathbb {X}-N]$ is well defined. To attack the questions on existence and deformation along the 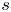 $s$ direction, we introduce the inducing method. Sufficient and necessary conditions are given, for a stability condition on an
$s$ direction, we introduce the inducing method. Sufficient and necessary conditions are given, for a stability condition on an 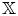 $\mathbb {X}$-baric heart (that is, a usual triangulated category) of
$\mathbb {X}$-baric heart (that is, a usual triangulated category) of 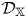 $\mathcal {D}_\mathbb {X}$ to induce
$\mathcal {D}_\mathbb {X}$ to induce 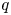 $q$-stability conditions on
$q$-stability conditions on 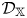 $\mathcal {D}_\mathbb {X}$. As a consequence, we show that the space
$\mathcal {D}_\mathbb {X}$. As a consequence, we show that the space 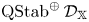 $\operatorname {QStab}^\oplus \mathcal {D}_\mathbb {X}$ of (induced) open
$\operatorname {QStab}^\oplus \mathcal {D}_\mathbb {X}$ of (induced) open 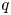 $q$-stability conditions is a complex manifold of dimension
$q$-stability conditions is a complex manifold of dimension 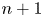 $n+1$. Our motivating examples for
$n+1$. Our motivating examples for 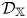 $\mathcal {D}_\mathbb {X}$ are coming from (Keller's) Calabi–Yau-
$\mathcal {D}_\mathbb {X}$ are coming from (Keller's) Calabi–Yau-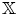 $\mathbb {X}$ completions of dg algebras. In the case of smooth projective varieties, the
$\mathbb {X}$ completions of dg algebras. In the case of smooth projective varieties, the 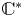 $\mathbb {C}^*$-equivariant coherent sheaves on canonical bundles provide the Calabi–Yau-
$\mathbb {C}^*$-equivariant coherent sheaves on canonical bundles provide the Calabi–Yau-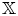 $\mathbb {X}$ categories. Another application is that we show perfect derived categories can be realized as cluster-
$\mathbb {X}$ categories. Another application is that we show perfect derived categories can be realized as cluster-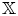 $\mathbb {X}$ categories for acyclic quivers.
$\mathbb {X}$ categories for acyclic quivers.