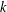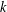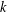Refine search
Actions for selected content:
5 results
2 - The Language of Homology
-
- Book:
- Homological Methods in Banach Space Theory
- Published online:
- 19 January 2023
- Print publication:
- 26 January 2023, pp 46-127
-
- Chapter
- Export citation
PERIODIC
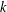 $k$-GRAPH ALGEBRAS REVISITED
$k$-GRAPH ALGEBRAS REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 20 April 2015, pp. 267-286
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
A universality result for endomorphism monoids of some ultrahomogeneous structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 635-656
-
- Article
-
- You have access
- Export citation
Amalgamations of Categories
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 2 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 273-284
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
Categorical constructions in C*-algebra theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-114
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation