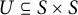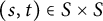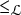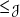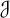We continue our study from Peterzil et al. (2022, Preprint, arXiv:2208.08293) of finite-dimensional definable groups in models of the theory $T_{\partial }$, the model companion of an o-minimal ${\mathcal {L}}$-theory T expanded by a generic derivation $\partial $ as in Fornasiero and Kaplan (2021, Journal of Mathematical Logic 21, 2150007).

We generalize Buium’s notion of an algebraic D-group to ${\mathcal {L}}$-definable D-groups, namely $(G,s)$, where G is an ${\mathcal {L}}$-definable group in a model of T, and $s:G\to \tau (G)$ is an ${\mathcal {L}}$-definable group section. Our main theorem says that every definable group of finite dimension in a model of $T_\partial $ is definably isomorphic to a group of the form

$$ \begin{align*}(G,s)^\partial=\{g\in G:s(g)=\nabla g\},\end{align*} $$

for some ${\mathcal {L}}$-definable D-group $(G,s)$ (where $\nabla (g)=(g,\partial g)$).

We obtain analogous results when T is either the theory of p-adically closed fields or the theory of pseudo-finite fields of characteristic $0$.

A semigroup S is said to be right pseudo-finite if the universal right congruence can be generated by a finite set 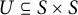$U\subseteq S\times S$, and there is a bound on the length of derivations for an arbitrary pair 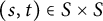$(s,t)\in S\times S$ as a consequence of those in U. This article explores the existence and nature of a minimal ideal in a right pseudo-finite semigroup. Continuing the theme started in an earlier work by Dandan et al., we show that in several natural classes of monoids, right pseudo-finiteness implies the existence of a completely simple minimal ideal. This is the case for orthodox monoids, completely regular monoids, and right reversible monoids, which include all commutative monoids. We also show that certain other conditions imply the existence of a minimal ideal, which need not be completely simple; notably, this is the case for semigroups in which one of the Green’s preorders 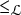${\leq _{\mathcal {L}}}$ or 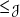${\leq _{\mathcal {J}}}$ is left compatible with multiplication. Finally, we establish a number of examples of pseudo-finite monoids without a minimal ideal. We develop an explicit construction that yields such examples with additional desired properties, for instance, regularity or 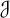${\mathcal {J}}$-triviality.