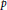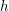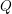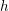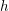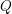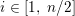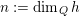5 results
Incompressibility of Products of Pseudo-homogeneous Varieties
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 824-833
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
Hermitian forms over quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 2073-2094
- Print publication:
- December 2014
-
- Article
- Export citation
Generically split projective homogeneous varieties. II
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 1-8
- Print publication:
- August 2012
-
- Article
- Export citation
Incompressibility of quadratic Weil transfer of generalized Severi–Brauer varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 12 May 2011, pp. 119-131
- Print publication:
- January 2012
-
- Article
- Export citation
Connectedness of classes of fields and zero-cycles on projective homogeneous varieties
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 24 November 2006, pp. 1522-1548
- Print publication:
- November 2006
-
- Article
-
- You have access
- Export citation