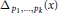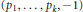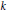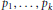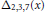Refine search
Actions for selected content:
3 results
WEIGHT ELEMENTS OF THE KNOT GROUPS OF SOME THREE-STRAND PRETZEL KNOTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 305-318
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Erratum: The Lehmer Polynomial and Pretzel Links
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 2 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, p. 231
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation
The Lehmer Polynomial and Pretzel Links
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 4 / 01 December 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 440-451
- Print publication:
- 01 December 2001
-
- Article
-
- You have access
- Export citation